힙 (Heap)
Heap 🙂
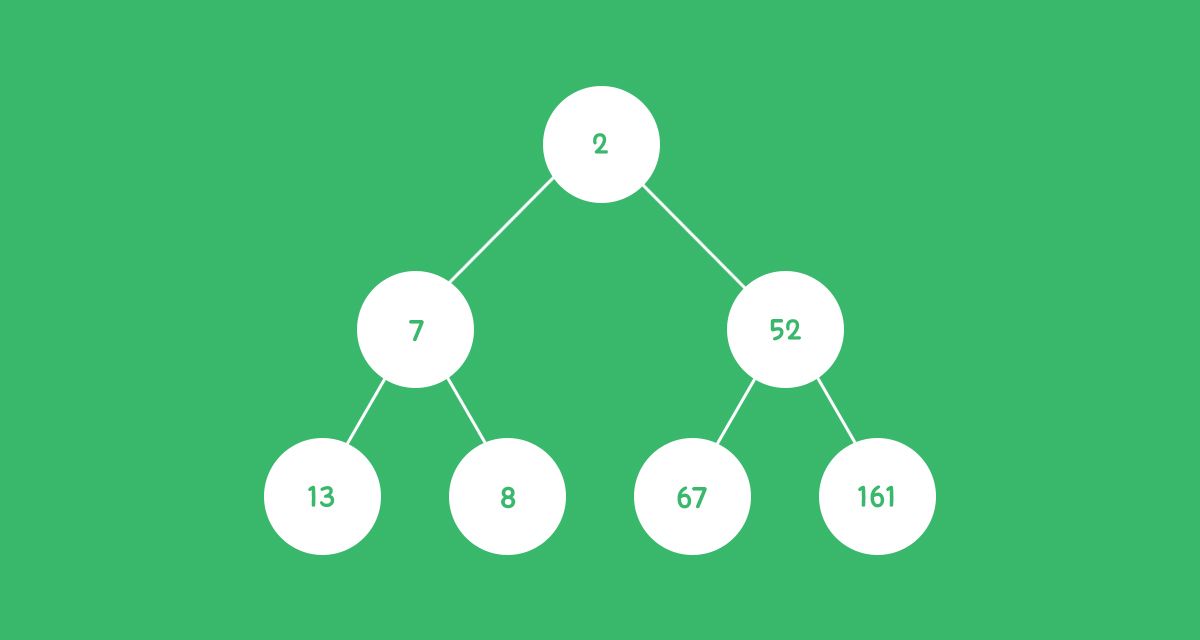
힙(Heap)은 트리 내에서 가장 크거나 작은 값을 루트로 가진 완전 이진 트리를 말합니다. 가장 작은 값이 루트로 오는 경우를 최소힙(Min-Heap)이라 말하며, 반대로 가장 큰 값이 오는 경우는 최대힙(Max-Heap)이라 합니다. 힙은 큐에서 나올 요소에 대해 우선순위를 적용하는 우선순위 큐를 만들 때와 힙을 통한 정렬인 힙 정렬에 활용할 수 있습니다. 루트가 가진 값이 기본적으로 최솟값 또는 최댓값이기 때문에 이런 활용들이 가능한 것입니다. 우선순위 큐는 이후의 포스트를 통해 소개하겠습니다.
힙은 새로운 요소를 추가하거나 제거할 때, 힙을 재구성해야 하므로 리스트보다는 배열로 만드는 편입니다.
노드 & 클래스 생성
function Node(data) {
this.data = data;
}
function Heap({ type }) {
Array.call(this);
this.usedSize = 0;
this.type = type;
}
Heap.prototype = Object.create(Array.prototype);
Heap.prototype.constructor = Heap;힙을 배열로 만들 것이기 때문에, Array를 상속 받아 배열처럼 사용할 수 있도록 했습니다. 프로토타입 상속 시에는 생성자 내에서 항상 부모 프로토타입을 호출해 컨텍스트가 자기 자신을 가리킬 수 있도록 해야 합니다. 그리고 매개변수 type의 값에 따라 최소힙 또는 최대힙으로 사용할 수 있게끔 만들었습니다.
노드 추가
Heap.prototype.insert = function (newData) {
let currentIndex = this.usedSize;
let parentIndex = this.getParentIndex(currentIndex);
this.push(newData);
this.usedSize += 1;
if (this.type === 'min') {
// min-heap
while (currentIndex > 0 && this[currentIndex].data < this[parentIndex].data) {
this.swap(currentIndex, parentIndex);
currentIndex = parentIndex;
parentIndex = this.getParentIndex(currentIndex);
}
} else {
// max-heap
while (currentIndex > 0 && this[currentIndex].data > this[parentIndex].data) {
this.swap(currentIndex, parentIndex);
currentIndex = parentIndex;
parentIndex = this.getParentIndex(currentIndex);
}
}
};힙에 새로운 데이터를 추가하는 것은 간단하지만, 후처리를 잘 해줘야 합니다. 먼저 배열의 마지막에 새로운 데이터를 추가한 다음, 반복문을 통해 부모 요소와 값을 비교하며 교환할 수 있는지 체크합니다. 과정을 반복하면서 계속 올라가야 하므로, 현재 포지션과 부모 포지션의 값을 계속 갱신해야 합니다. 이렇게 힙 구성이 완료되면, 마지막에 힙에 들어 있는 요소 개수를 의미하는 usedSize를 하나 증가시키면서 마무리합니다.
루트 제거
Heap.prototype.delete = function () {
const deleteNode = this[0];
this.usedSize -= 1;
if (this.usedSize === 0) {
this.pop();
return deleteNode;
} else {
this[0] = this.pop();
}
// Reconstruct heap
let parentIndex = 0;
let leftChildIndex = this.getLeftChildIndex(parentIndex);
let rightChildIndex = leftChildIndex + 1;
while (true) {
let selectedIndex;
if (leftChildIndex >= this.usedSize) break;
if (rightChildIndex >= this.usedSize) {
selectedIndex = leftChildIndex;
if (this.type === 'min') {
if (this[selectedIndex].data < this[parentIndex].data) {
this.swap(selectedIndex, parentIndex);
parentIndex = selectedIndex;
} else {
break;
}
} else {
if (this[selectedIndex].data > this[parentIndex].data) {
this.swap(selectedIndex, parentIndex);
parentIndex = selectedIndex;
} else {
break;
}
}
} else {
if (this.type === 'min') {
if (this[leftChildIndex].data < this[rightChildIndex].data) selectedIndex = leftChildIndex;
else selectedIndex = rightChildIndex;
if (this[selectedIndex].data < this[parentIndex].data) {
this.swap(selectedIndex, parentIndex);
parentIndex = selectedIndex;
} else {
break;
}
} else {
if (this[leftChildIndex].data > this[rightChildIndex].data) selectedIndex = leftChildIndex;
else selectedIndex = rightChildIndex;
if (this[selectedIndex].data > this[parentIndex].data) {
this.swap(selectedIndex, parentIndex);
parentIndex = selectedIndex;
} else {
break;
}
}
}
leftChildIndex = this.getLeftChildIndex(parentIndex);
rightChildIndex = leftChildIndex + 1;
}
return deleteNode;
};단 하나의 요소만 존재하면, 값을 반환하면서 힙을 비우면 됩니다. 하지만 두 개 이상의 요소가 힙 안에 있다면, 이에 따른 후처리가 필요합니다. 먼저 루트를 제거함과 동시에 가장 마지막 요소를 루트 위치로 가져 옵니다. 이후 양쪽의 자식들과 값을 비교하며, 교환이 가능하면 교환하는 식으로 반복문을 통해 처리합니다.
유틸 메소드
Heap.prototype.swap = function (index1, index2) {
[this[index1], this[index2]] = [this[index2], this[index1]];
};
Heap.prototype.getParentIndex = function (index) {
return Math.floor((index - 1) / 2);
};
Heap.prototype.getLeftChildIndex = function (index) {
return index * 2 + 1;
};유틸 메소드는 반복적으로 사용되는 코드를 재사용 할 수 있도록 만든 것입니다.
References 📝
본문의 내용은 GeeksforGeeks의 Heap 자료를 참고해 작성했습니다 ❤️
'💻 컴퓨터공학 > 자료구조' 카테고리의 다른 글
| 해시 테이블 (Hash Table) (0) | 2021.11.01 |
|---|---|
| 우선순위 큐 (Priority Queue) (0) | 2021.10.30 |
| 분리 집합 (Disjoint Set) (0) | 2021.10.26 |
| 수식 트리 (Expression Tree) (0) | 2021.10.26 |
| 이진 트리 (Binary Tree) (0) | 2021.10.26 |
댓글
이 글 공유하기
다른 글
-
해시 테이블 (Hash Table)
해시 테이블 (Hash Table)
2021.11.01 -
우선순위 큐 (Priority Queue)
우선순위 큐 (Priority Queue)
2021.10.30 -
분리 집합 (Disjoint Set)
분리 집합 (Disjoint Set)
2021.10.26 -
수식 트리 (Expression Tree)
수식 트리 (Expression Tree)
2021.10.26